神奇的6174
首先,在心裡想著四位數,可以是TA的生日、你們的紀念日。或者是任意一個不完全相同的四位數(不能是1111、2222……)。然後,重新排列這個四位數。
從大到小排列獲得最大的四位數;從小到大排列獲得最小的四位數。
最後,用最大的四位數減去最小的四位元數,獲得新數字,並對每個新數字繼續重複上述操作。
下面實操一波,小編舉個浪漫的例子:1314。

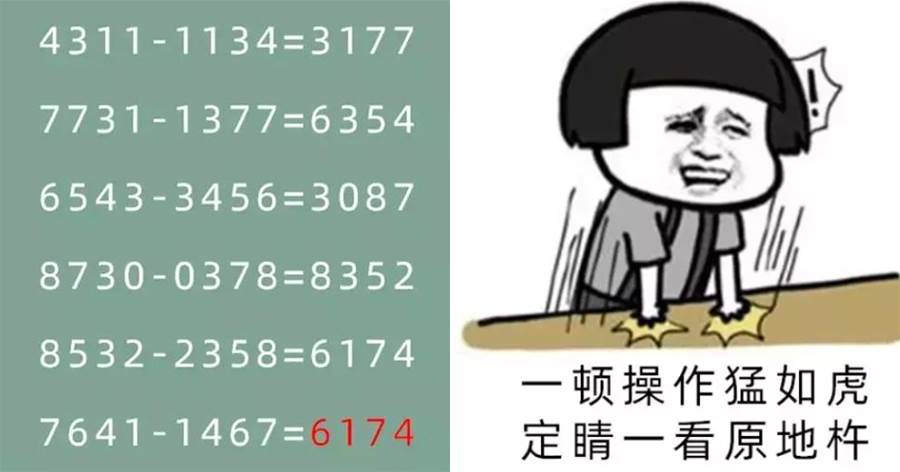
一頓操作之後,發現無論再怎麼算下去,結果都停留在6174。

於是小編對300個不同的四位數進行上述操作,進行了嚴謹的驗證,結果發現:這300個不同的四位數中,均不超過七步操作,得出的結果就停留在6174,無法跳出來。
這個神奇的6174就是跳不出來的黑洞數(陷阱數)。
6174的由來
那麼,這麼有趣的數是誰發現的呢?
正是印度數學家卡普列加提出的。

卡普列加,印度知名的休閒數學家,印度孟買大學本科畢業,沒有讀過研究生,職業就是一名老師,可謂是資歷平平。
但是,卡普列加卻對數位的屬性非常感興趣,而且他一生中還發現了不少有趣的數字。
1949年,一個風雨交加的晚上,卡普列加改完學生的作業,無心睡眠,一邊看著窗外的閃電,一邊拿著筆在草稿紙上進行計算,白天給同學們講了交換律知識點的他突發奇想:如果一個多位數,對變換數位順序得出的大小值再作運算反覆運算會怎麼樣呢?
經過多次的加減乘除反覆運算計算,連學生的作業本都拿來做草稿紙了,他終於發現:
一個不完全相同的四位數,重新排列四位元數中的四個數字得到最大和最小值,再作減法,最多7次反覆運算,都會得到6174這個神奇的數字!
與此同時,卡普列加還發現三位數的黑洞數495。
小編用211來試一下:

然而,這些有趣的數並得不到當時印度數學界的認可,只能在低水準的數學期刊或者私人期刊發佈。
印度的科學家們都覺得卡普列加太民科了,沒有數學家願意跟他交流,很多時候都是自個玩兒。

直到1975年,美國的科普作家馬丁加德納(Martin Gardner)在頗有名氣的科學數學遊戲專欄提到了卡普列加的成果,引起了美國數學家們的興趣,卡普列加因此聞名世界。
卡普列加發現的數位屬性,也開始成為了許多數學家的研究課題。
自然數這麼多,數位黑洞還有其他數位嗎?
數學黑洞還有哪些?
有,當然有!
比如說「13」。
任意取一個自然數;然後每一位上的數相加起來;得到的結果乘以3再加上1得到一個新的數;重複執行上述操作;最終的結果必定是13。
我們就隨便用9257舉個例子:

還有「153」。
隨意選取一個自然數,要求是3的倍數;求每一個位數的立方數,把它們加起來得到一個新的數;重複上述操作;
就用207來試試水吧:

其實「153」在數論中,還有一個別稱——自戀數:
對於任意一個n位數,每一位數的n次方之和為這個數的本身,很明顯,「153」就是這樣的數。
這樣的自戀數還有嗎?
很明顯,1位數都是;兩位數沒有;三位數有4個,153是最小的,還有370、371、407四位數有3個,1634、8208、9474,自戀數是不是有限個的呢?
是的,很早就有人輕易證明出,自戀數不會超過61位數,假如存在一個61位數,61個9^3之和得到的數還沒有這個數的本身大。最大的自戀數是一個39位數:115132219018763992565095597973971522401。



















