
這種問題經常在網路上出現,很容易讓人陷入某種誤區,甚至讓人患上「強迫症」。看到無理數就會產生某種說不清道不明的「歧視」心理,就好像無理數真的「無理」一樣,「無理數」這三個字確實蒙蔽了很多人的雙眼!
事實上無理數一點也不「無理」,無理數和有理數完全是平等的,都是一個再普通不過的數,而且是真實存在的數,一個非常確定的數。
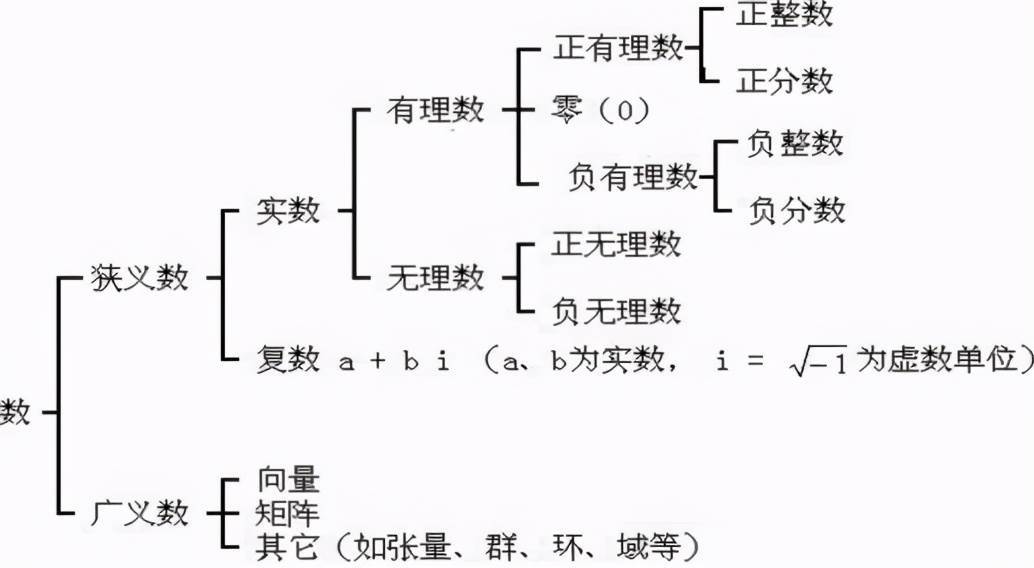
無理數與有理數的區別只有一點:無限不迴圈,僅此而已。但你不能因為無限不迴圈就對無理數「另眼看待」,甚至會下意識地認為「無限不迴圈就不是確定的數」!
不少人總是下意識習慣性地強迫無理數必須用小數完全寫出來,寫不出來心裡就憋得慌。但一個非常現實的問題是:為何一定要用小數寫出來呢?用其他形式寫出來不行嗎?
這就是不少人認識上的誤區!

比如說圓周率π就是π,就好比「1就是1」一樣,都是一個確定的數。我可以很輕鬆地把π寫出來,它就是:π。
明白了這點,再回到問題中。
1/3等於0.333......,永遠寫不完,但寫不完不代表1/3就不存在,事實上你可以非常輕鬆地在數周上畫出1/3長度,不但如此,你可以在數周上畫出任何一個數(包括無理數)的長度,比如說π,√2等。
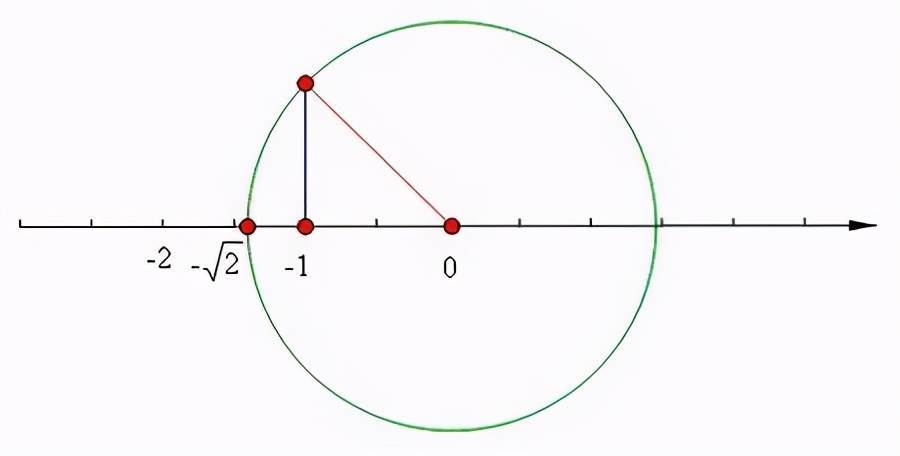
下圖一眼就能看出如何在數軸上畫出√2:畫一個直角邊為1的等腰直角三角形,然後以斜邊為半徑畫一個圓形,與數軸的交點就是√2。
確實,在人類數學史上,尤其是在微積分思想產生之前,無理數的概念困惑了很多人。就好題目中的問題一樣,0.333永遠寫不完,怎麼可能分成三等份呢?
首先1/3是一個確定的數,非常確定,是一個實數。只要是實數,都會對應數軸上的一個點。我們經常用到的圓周率π是無理數,它也對應數軸上一個點,π是一個確定的長度。
不少人認為無理數是不那麼確定的數,其實只是一種錯覺,一種心理暗示罷了,或者說是一種「強迫症」!
肯定有人會這樣質問:1米長的繩子分成三等份,一份的長度就是0.333......,那麼三份的長度應該是0.999......,也不等於1啊!這就是誤區所在,其中也牽扯到極限的思想。
最簡單的解釋就是:不要總是在0.
333......(一直迴圈)上面較真,你直接認為1/3不就行了嗎?1/3乘以3不正好等於1嗎?為什麼非要把任何數都要寫成小數的形式才甘心呢?

但總會有人不甘心,一定要用小數寫出來才甘休。所以問題的關鍵就在於:0.999......是否等於1?
0.999......等於1,0.999......等於1,0.999......等於1。重要的事情說三遍!
可以用反證法來證明,首先假設0.999......不等於1,由於兩個不相等的數之間肯定會存在無數多個數,這意味著0.999......和1之間存在無數多個數,但事實上不要說找到無數多個數了,你能找到哪怕一個數嗎?
如果能找到,0.999......當然不等於1,如果找不到,0.
999......必然等於1。最後的結果是:你不得不承認0.999......等於1。雖然你可能還是那麼不甘心!
還有人經常會這樣問:0.999......不是比1要小0.00000......1嗎?極限屬於一種抽象概念,非具體的,所以我們不能用具體數值的加減來理解。
最後還要強調一點,純理論上分析,一根一米長的繩子可以分成三等份,但現實中你永遠做不到。這與科技發達與否沒有關係,科技再發達也不可能做到,誤差是永遠存在的。

而且「一根一米長的繩子分成三等份」僅僅是從數學概念來分析的,也就是說數軸上長度為1的線段可以分成三等份。但數學並不等同于現實,數學可以說是抽象的概念,帶有絕對性。而測量屬於具體的,具有相對性。
同時,數學上不存在最小的數,你永遠找不到大於0的最小的數,但現實中存在最小的長度單位,它就是普朗克長度,任何小於普朗克長度的單位都沒有意義!



















